CSAPP 02 - Floating Point

Notes for Floating Point.

二进制小数

对于小数

$b_mb_{m-1} \dots b_1b_0.b_{-1}b_{-2} \dots b_{-n-1}b_{-n}$

其中 $b_i$ 取 0 或 1，则其值 $b$ 为

$b=\sum_{i=-n}^{m}2^{i} \cdot b_i$

在编码长度有限的条件下，这种表示法只能表示那些能被写成形如 $x \cdot 2^y$ 的数。而对于无法写成这种形式的数只能进行近似表示，如 1/5。

IEEE浮点表示

一个浮点数 $V$ 表示为

$V=(-1)^s \times M \times 2^E$

$s$ ：符号位，正数为1，负数为0。
$M$ ：尾数，取值为1 ~ 2 - ε 或 0 ~ 1 - ε 。
$E$ ：阶码，表示2的E次幂。

对这三部分进行编码：

一个单独的符号位直接编码 $s$ 。
$k$ 位阶码字段 $exp=e_{k-1} \dots e_1e_0$ 编码 $E$ 。
$n$ 位小数字段 $frac=f_{n-1} \dots f_1f_0$ 编码 $M$ 。

以C语言为例，各部分编码位数如图1

图1 C语言浮点数编码位数

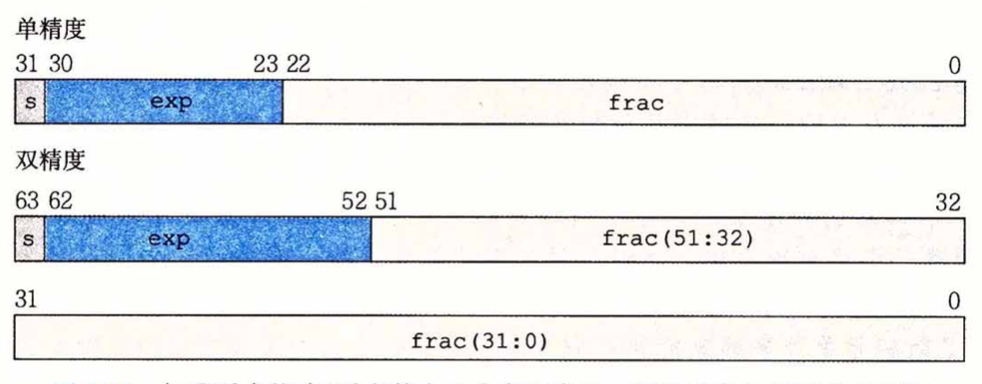
给定位表示，根据 $exp$ 的值，被编码的值可被分为三种情况，见图2（以单精度为例）

图2 单精度浮点数分类

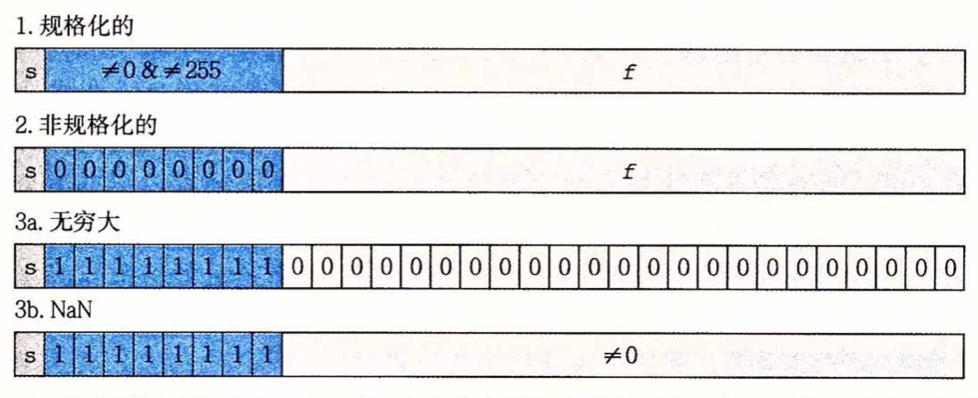
规格化的

阶码 $E=e-bias$ ，其中 $e=e_{k-1} \dots e_1e_0$ 是无符号数，$bias$ 是一个等于 $2^{k-1}-1$ 的偏置值（单精度即127），因此产生的指数范围是 -126 ~ 127。

尾数 $M=1+f$。
非规格化的

阶码 $E=1-bias$ ，尾数 $M=f$，此时尾数不包含隐含的1。非规格化数提供了浮点0的表示方法。
特殊值

当小数域全为0时，得到的值表示 $\infty$，根据符号位确定表示的是 $+\infty$ 还是 $-\infty$。

当小数域含有1时，得到的值表示 NaN，例如求 $\sqrt{-1}$ 就会得到这样的值。

舍入

当某个数 $x$ 无法用给定精度位数表示需要进行，为其找到一个最近的，能进行浮点表示的数代表它，这就是舍入运算。

舍入运算会遇到的一个问题是究竟应该向下舍入还是向上舍入，一种方法是同时计算上下界 $x^+$ 和 $x^-$，使得 $x^- \le x \le x^+$。

IEEE浮点格式定义了四种不同的舍入方式

向偶数舍入： 4 舍，6 入，5 向偶数。例如 1.5 和 2.5 均舍为 2，3.5 和 4.5 均舍为 4。
向零舍入： 正数下舍，负数上舍。
向上舍入： ceil
向下舍入： floor

向偶数舍入可以降低平均值计算时的误差，用于找到最接近的匹配。其他三种方法用于计算上下界。

对于向偶数舍入，在具体操作时，当最低精度位为0时视为偶数，为1时视为奇数。每次舍入都倾向于使得最低精度位变为0。

例如当最低精度位为四分之一位，即小数点后两位时，$10.11100_2(2 \frac{7}{8})$ 被舍入到 $11.00_2(3)$。而 $10.10100_2(2 \frac{5}{8})$ 被舍入到 $10.10_2(2 \frac{1}{2})$。

浮点运算

谨慎地对浮点运算使用结合律和分配律，尤其是在出现大数运算时。例如如下的程序

#include<cstdio>
using namespace std;

int main() {
    float a1 = (3.14 + 1e20) - 1e20, a2 = 3.14 + (1e20 - 1e20);
    printf("%f %f\n%f %f\n", a1, a2);
    return 0;
}

//0.000000 3.140000